1.6　情報理論

1.6.0

• p.49下「ちなみに、これ以上短い符号は使うことができない。なぜなら、結合した文字列を符号に分割する曖昧さを残してはならないからである。」
  ←曖昧さとは、例えば状態eに"11110"という符号を割り当てると、それぞれの符号そのものは区別でき平均符号長も短くなるが、例えば"1111010"という文字列は"11110 10"(eb)または"111101 0"(fa)と2通りの解釈ができてしまう
  
  
• N個の物体の箱への入れ方
  N個の物体に番号を付けるなど区別して並べる方法はN!通り。並べた物体を最初のn1個を1番目の箱に入れ、次のn2個の物体を2番目の箱に入れ、とやっていく。1番目の箱の中の物体の並びはn1!通りあって、1番目の箱の並びそれぞれに対して2番目の箱の中の並びはn2!通りあって、...となり箱の中の並びは区別しないで同じとみなすので、これらの積で総数を割る必要がある。よって

  mathjax

  mathjax

  \[ W=\frac{N!}{\prod_{i}^{} n_i!} \]

• 式(1.97)
  式(1.96)から

  mathjax

  \[ \ln{n_i!}\simeq n_i\ln{n_i}-n_i \]

• 式(1.99)あたり

  mathjax

  mathjax

  \begin{eqnarray} \tilde{H}&=&-\{p(x_1)\ln{p(x_1)}+p(x_2)\ln{p(x_2)}+\ldots+p(x_M)\ln{p(x_M)}\}\\ & & +\lambda\{p(x_1)+p(x_2)+\ldots+p(x_M)-1\} \end{eqnarray}

同様にして

また、

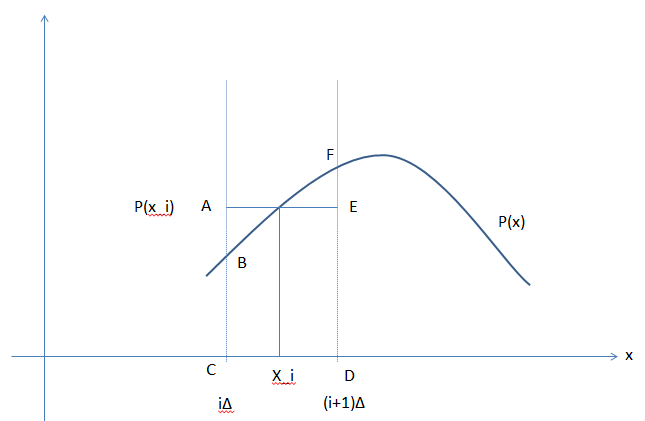
• (1.101)平均値の定理
  
  下図でBCDFの面積がACDEと等しくなるようなx_iが存在する。

• (1.108)あたり

  mathjax

  \[ \int_{-\infty}^{\infty}\{-p(x)\ln{p(x)}+\lambda_1p(x)+\lambda_2xp(x)+\lambda_3(x-\mu)^2p(x)\}\mathrm{dx}-(\lambda_1+\lambda_2\mu+\lambda_3\sigma^2) \\ =\int_{-\infty}^{\infty}F(x,p(x))\mathrm{dx}-(\lambda_1+\lambda_2\mu+\lambda_3\sigma^2) \]
  とすると

  mathjax

  \[ \frac{\partial F}{\partial p(x)} = -\ln{p(x)}-p(x)\frac{1}{p(x)}+\lambda_1+\lambda_2x+\lambda_3(x-\mu)^2=0 \]

  mathjax

  \[ p(x)=\mathrm{exp}\{-1+\lambda_1+\lambda_2x+\lambda_3(x-\mu)^2\} \]

• (1.112)

  mathjax

  \begin{eqnarray} \\ H[{\bf y}\mid{\bf x}] &=& -\iint p({\bf y},{\bf x})\ln{p({\bf y}\mid{\bf x})}\mathrm{d{\bf y}}\mathrm{d{\bf x}} \\ &=& -\iint p({\bf y},{\bf x})\ln{\frac{p({\bf y},{\bf x})}{p({\bf x})}}\mathrm{d{\bf y}d{\bf x}} \\ &=& -\iint \{p({\bf y},{\bf x})\ln{p({\bf y},{\bf x})}-p({\bf y},{\bf x})\ln{p({\bf x})}\}\mathrm{d{\bf y} d{\bf x}} \\ &=& -\iint p({\bf y},{\bf x})\ln{p({\bf y},{\bf x})}\mathrm{d{\bf y}d{\bf x}}+\int p({\bf x})\ln{p({\bf x})}\mathrm{d{\bf x}} \\ &=& H[{\bf x},{\bf y}]-H[{\bf x}] \end{eqnarray}

1.6.1　相対エントロピーと相互情報量

• TODO:演習1.36
• TODO:データ圧縮と密度推定（・・・）は密接に関係しており・・・: ？？？

  br

   

  br

   

  br